November 23, 2021

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

In class 10 maths chapter 3 pair of linear equations in two variables, we will extend our knowledge of linear equations. In class IXth, we have studied the basics of linear equations in two variables and before that, we had learned about linear equations in one variable. There will be a lot of plotting on graph papers, therefore, if you are not very comfortable with graph papers, then this chapter will teach you well.

Just like we do with all our articles on 10th maths, we will first take a quick look at the summary or main points that we had studied in class 9th and then move on to our topics in class Xth. This chapter will look very difficult if you do not remember anything from the previous class as most of the topics build on the ones learned in the previous class.

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Let’s first get familiar with the command terminologies that we will need in this chapter and then move on to the summary from the previous class.

What are linear equations?

Linear equations are simply algebraic expressions (like polynomials) that are written for different variables. Note that the equation must not have a degree greater than 1. e.g: x+1 = 0, 2y+2 = 0, 3z+5y-4 = 0, etc.

What is a linear equation in one variable?

The linear equation that has only one variable in it is called a linear equation in one variable. e.g 6y+5=0, 7x+2=0, etc.

What is a linear equation in two variables?

The linear equation that has two variables in it is called a linear equation in two variables. e.g 6y+5x=0, 7x+2z=0, etc.

Now that we have a basic understanding of some general terms needed for this chapter, let’s take a look at the summary of the previous class.

Technically, an equation which is in the form ax+by+c=0 and where, a, b, and c are real numbers and a & b are not zero, then it is called a linear equation.
A linear equation in two variables will have infinite solutions.
When plotting on a graph, a linear equation in two variables will always form a straight line.
x = 0 and y = 0 are the equations on y-axis and x-axis respectively.
The graph of x = a and y = a is always parallel to the y-axis and x-axis respectively.
If there is an equation of type y = mx, then this means that it is a line that will pass through the origin.
Every point that gets drawn on the graph of linear equations in two variables is a solution to it, and vice versa.

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables – Explanation part 1

With the above-given summary, things must have gotten a bit clear to you by now. If not, then consider quick revision of chapter 4 of class 9th. Now, let’s move on to the main topics of class 10 maths chapter 3 pair of linear equations in two variables.

# Pair of linear equations in two variables

When there are two linear equations that are in the same two variables, then is called a pair of linear equations in two variables. Following is the most common form of these types of equations.

$a_1x+b_1y+c_1=0$
$a_2x+b_2y+c_2=0$
where $a_1, a_2, b_1, b_2, c_1, c_2$ are ream numbers in such a way that $a_1^2+b_1^2\neq0$ , $a_2^2+b_2^2\neq0$

# Solving pair of linear equations in two variables using Graphical Method

On the graph, the pair of linear equations is represented by two lines. Following are the different scenarios for these two lines.

The pair of equations is consistent if the lines drawn on the graph intersect each other at a point. And, that point gives the unique solution of the two equations.
If the lines coincide, it can be said that there exist infinitely many solutions for those equations. In this case, each point on the line is the solution of these equations and the pair of equations will be called dependent (consistent).
And finally, if the lines do not intersect each other at any points i.e if the lines are parallel, then the pair of equations has no solutions and will be called inconsistent.

# Solving Pair of linear equations using an algebraic method

There are basically 3 methods to solve a pair of linear equations in algebra:

Substitution method: In this, we substitute the value of one variable by expressing it in terms of the other variable.
Elimination method: In this, we first eliminate one variable in order to get a linear equation in one variable.
Cross-multiplication method: In this, we use the cross multiplication technique to solve the equation.

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables – Explanation part 2

If there are two linear equations $a_1x+b_1y+c_1=0$ and $a_2x+b_2y+c_2=0$ , then there can be the following situation:

if $\frac{a_1}{a_2}\neq\frac{b_1}{b_2}$ , then the pair of linear equations is called consistent.
if 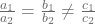$\frac{a_1}{a_2}=\frac{b_1}{b_2}\neq\frac{c_1}{c_2}$ , then the pair is called inconsistently.
and if 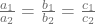$\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}$ , then the pair is called depending and consistent.

Now there can be many situations where equations are not linear, but we can perform certain operations on them to make them a pair of linear equations and then solve them.

This covers all important topics for class 10 maths chapter 3 pair of linear equations in two variables. Now, let’s see the blueprint of chapter 3.

Maths Chapter 3 Blueprint For class 10 (Pair of linear equations in two variables)
1 Marker	2 question
5 Marker	1 question
Total questions	3
Total marks	7

Note: The above-given table should be taken as a basic idea of how many questions will come in the exam from this chapter, in board exams, the number of questions and their marking may vary. Students should prepare for the worst-case scenario.

As you can see in the table, there will be 2 questions for 1 mark each and a 5 marks question, this will make this chapter worth 7 marks for 3 questions.

Book Solutions

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables – Explanation part 1

Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables – Explanation part 2

recomended for you